В предыдущих разделах вопросам определения областей устойчивости дискретных операторов не уделялось достаточного внимания. Во всех приведенных выше примерах область устойчивости можно найти аналитически, где-то относительно просто, где-то проявив изобретательность. Подробное описание соответствующих выкладок увело бы повествование в сторону от основных обсуждаемых проблем, связанных с диссипативными и дисперсионными характеристиками численных методов.
Диссипативные и дисперсионные поверхности дискретных операторов имеет смысл изучать только в областях их устойчивости. Интерполяционно-характеристический подход позволяет сформулировать геометрически наглядный признак устойчивости, который в большинстве случаев для схем второго порядка оказывается верным.
Как было подробно описано ранее, при интерполяционно-характеристическом подходе по известным на текущем временном слое значениям сеточной функции в заданном наборе точек с известными координатами строится полином Лагранжа. Этот многочлен может быть как интерполяционным, так и экстраполяционным.В первом случае координаты точки, в которой ищется приближенное значение, не должны выходить за пределы шаблона, на котором строится полином. Во втором случае - эта точка должна находиться вне этих пределов.
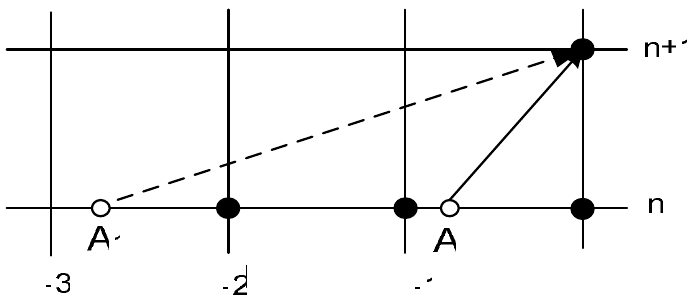
Отсюда и следует геометрический признак устойчивости: если точка A пересечения с временным слоем \(n\) обратной характеристики, выпущенной из акцепторного узла, при числе Куранта \(r\) оказывается в пределах шаблона, на котором построен полином Лагранжа, то это число \(r\), с большой вероятностью, принадлежит области устойчивости оператора. Если же эта точка выходит за пределы этого шаблона, то с большой вероятностью схема при этом числе Куранта будет неустойчива.
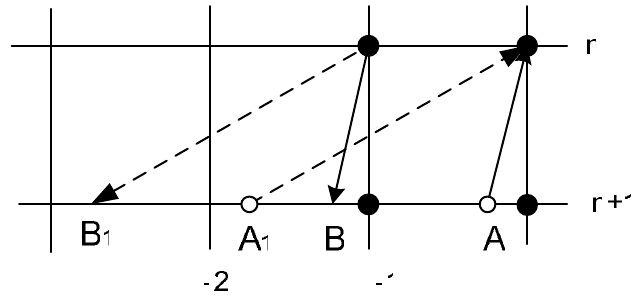
В качестве примера рассмотрим явную схему Бима-Уорминга и неявную схему Карлсона (рис. 27). Видно, что при числах Куранта, больших двойки, точка A1 лежит за пределами шаблона из точек \(\left(i,i-1,i-2\right)\), который для схемы Бима-Уорминга является стационарным. Это область неустойчивости. В неявной схеме Карлсона интерполяционный шаблон \(\left(i,i-1,B\right)\) зависит от числа Куранта, и изменяется таким образом, что точка пересечения обратной характеристики с временным слоем \(n\)всегда оказывается внутри шаблона. Схема безусловно устойчива.
 |
 |
| Рис. 27 | |
Геометрический признак устойчивости позволяет в автоматическом режиме формировать интервалы изменений чисел Куранта, претендующие на статус областей устойчивости. Далее этот статус может быть подтвержден или отвергнут либо аналитическими выкладками, либо численно - построением диссипативных поверхностей. Если все точки диссипативной поверхности не превышают единицу, то схема является устойчивой.
Следует отметить, что критерий устойчивости, основанный на анализе поведения частных решений, является только необходимым условием устойчивости. Для получения достаточных условий следует анализировать поведение численного решения в целом в подходящих функциональных пространствах.
Устойчивые схемы являются, как правило, диссипативными. Если по таким схемам проводить расчет в обратном направлении времени, то они окажутся неустойчивыми. Действительно, если при прямом течении времени амплитуда какой-либо гармоники на каждом шаге по времени уменьшается, то при его обратном течении она будет возрастать. Если дискретный оператор бездиссипативен, то он будет устойчив как при прямом, так и при обратном течении времени.
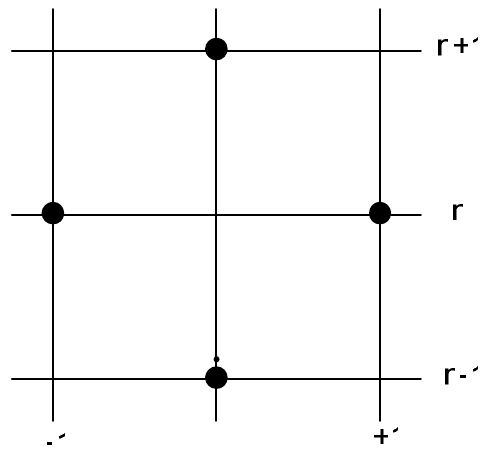
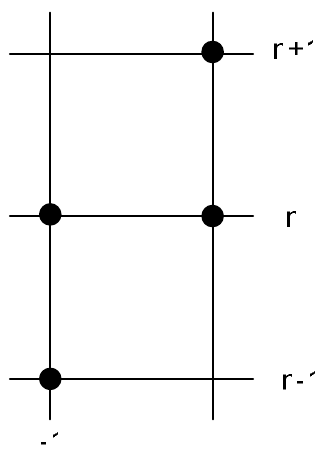
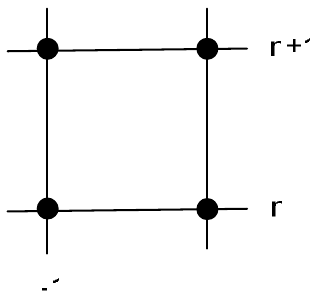
На рис. 28 приведены шаблоны бездиссипативных разностных схем - схемы «крест», КАБАРЕ, схемы Карлсона и схема Абрашина-Самарского.
 |
 |
 |
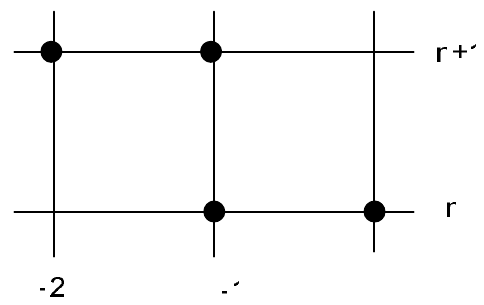 |
| Рис. 28 | |
Нетрудно видеть, что у этих шаблонов есть одно общее свойство - они обладают центральной симметрией. Покажем, что этот признак является и критерием. Действительно, изменение течения времени на обратное соответствует инверсии расчетной сетки относительно оси \(x\). Кроме того, при изменении направления времени скорость переноса меняет знак. Чтобы оставить скорость положительной, нужно отразить расчетную сетку относительно оси \(t\). Суперпозиция этих двух сеточных отражений приводит к отображению с центральной симметрией. Вычислительный шаблон при этом также преобразуется в центрально-симметричный. Если исходный шаблон обеспечивал бездиссипативность, то центрально - симметричный шаблон должен совпадать с исходным. Таким образом, вычислительные шаблоны обратимых по времени дискретных операторов должны обладать центральной симметрией.