Характеристическое уравнение неявной схемы Карлсона является линейным:
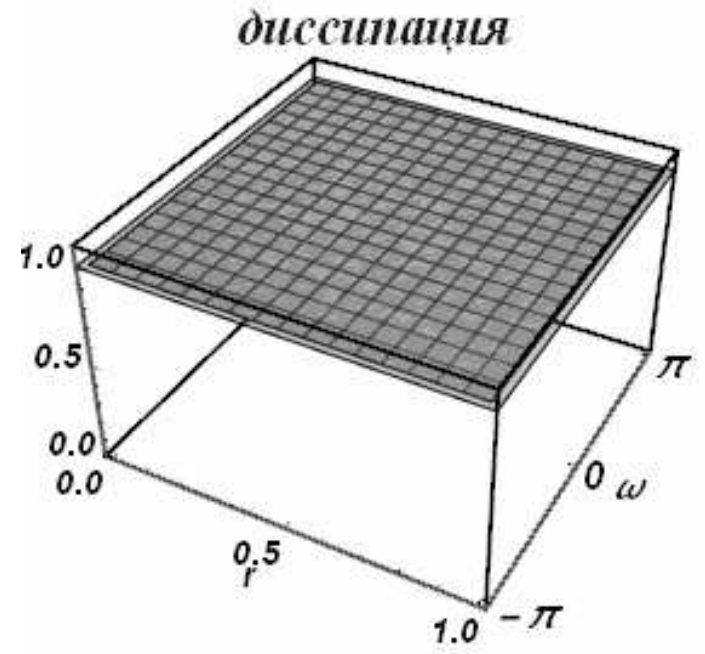
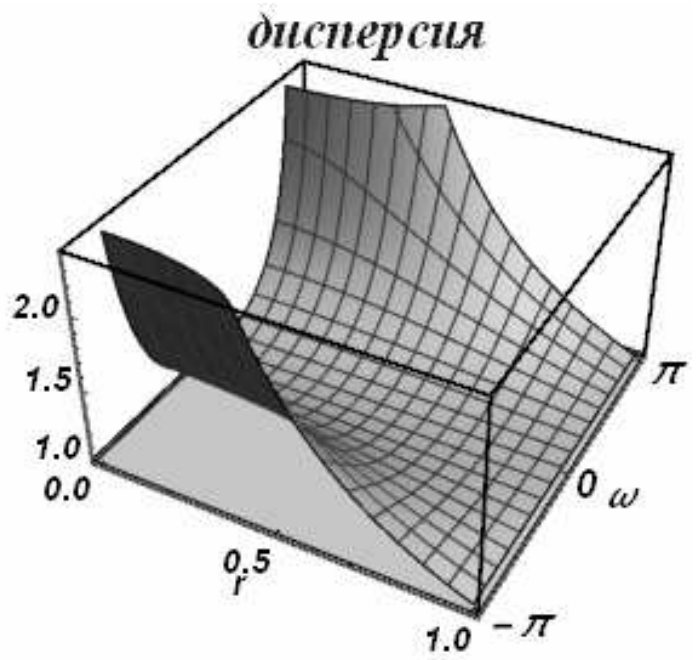
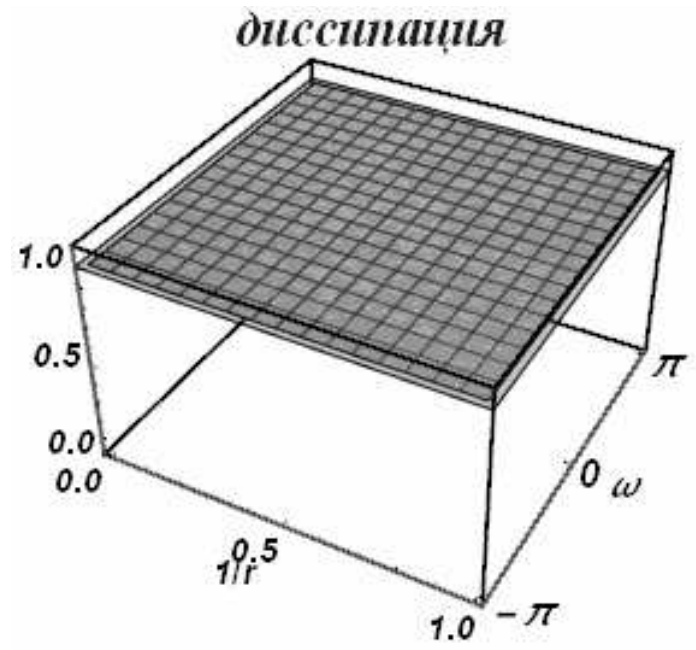
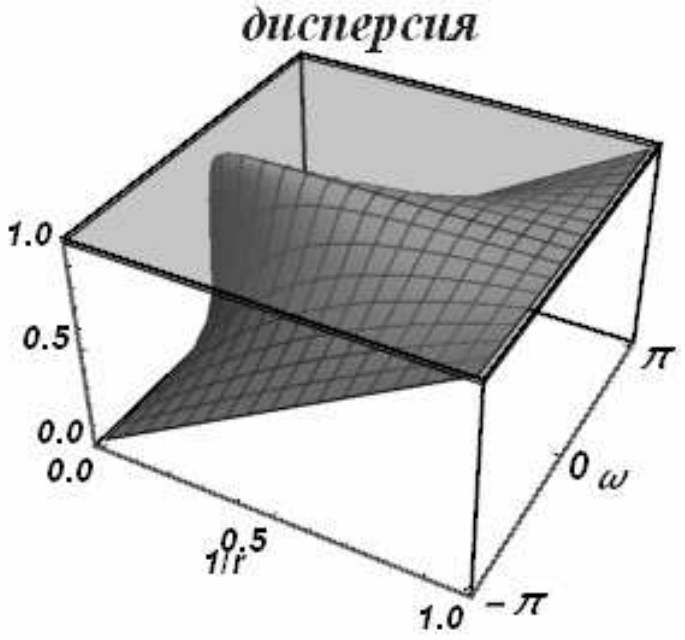
Можно показать аналитически, что модуль перехода \(\left|q\right|\) меньше или равен единице при всех положительных числах Куранта. Строить диссипативные и дисперсионные поверхности на бесконечной полуоси не представляется возможным, поэтому область устойчивости делится на две подобласти. Первая соответствует числам Куранта \(0\le r\le 1\), и в этой области поверхности выглядят обычным образом (рис. 21). Вторая подобласть \(1\le r\le \infty\) отображается на единичный отрезок заменой r на \({1\mathord{\left/ {\vphantom {1 r}} \right. } r}\)переходит в ноль, а единица остается единицей. На рис. 22 приведены диссипативная и дисперсионная поверхности на этом интервале.
 |
 |
| а) | б) |
| Рис. 21 | |
 |
 |
| а) | б) |
| Рис. 22 | |
Во всей области устойчивости модули перехода всех гармоник равны единице. Схема Карлсона бездиссипативна. При всех числах Куранта она проявляет аномальные дисперсионные свойства.
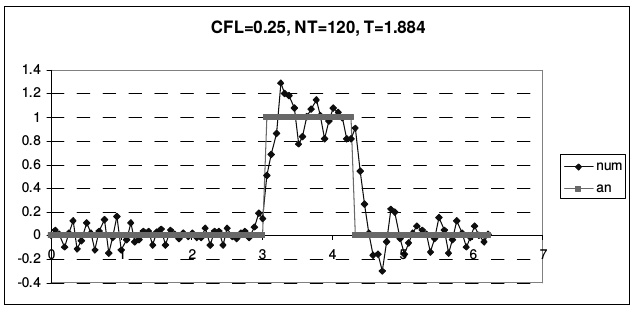
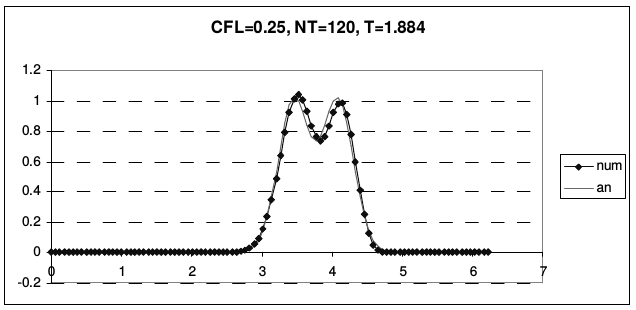
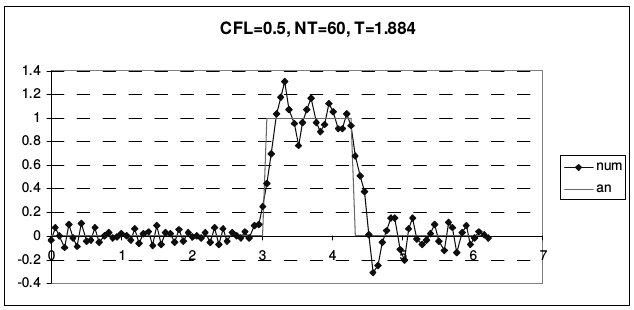
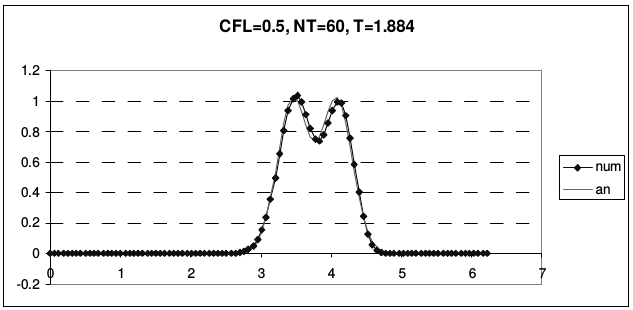
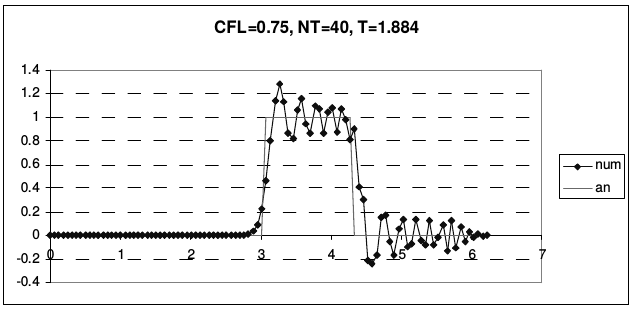
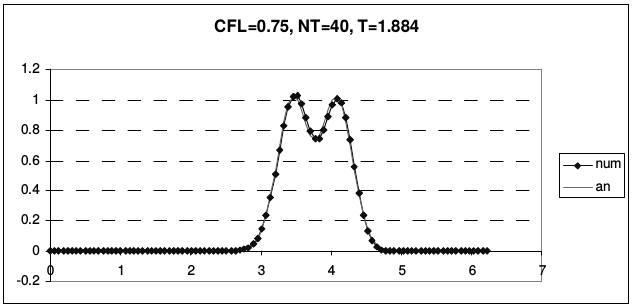
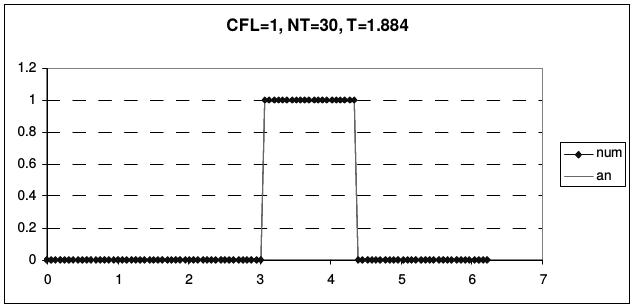
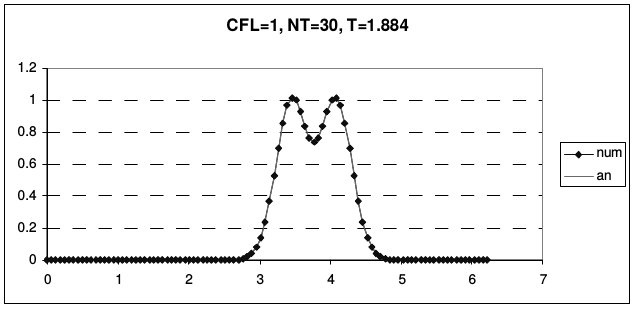
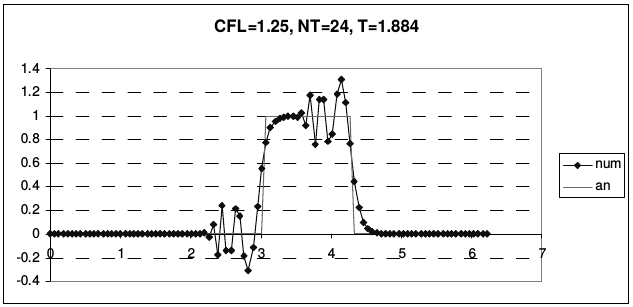
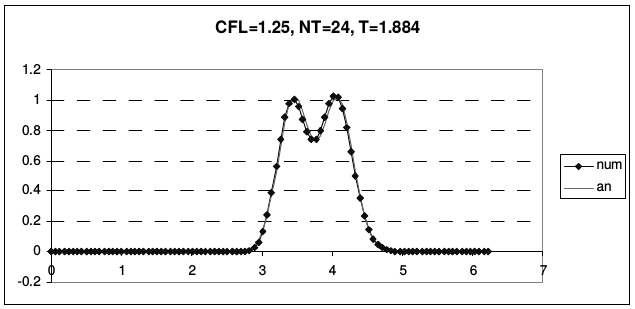
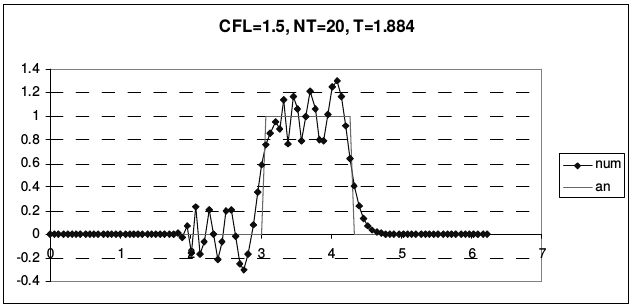
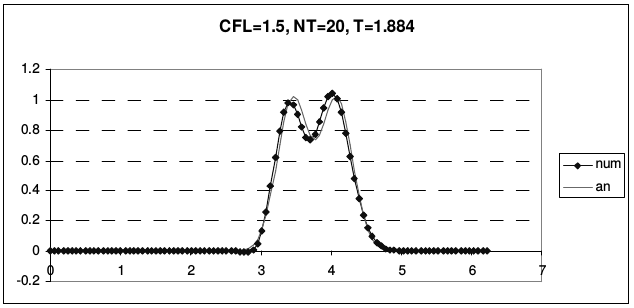
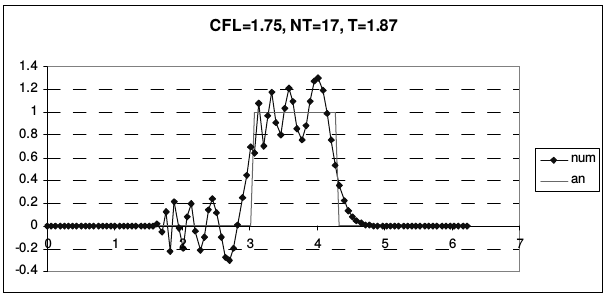
Рис. 23 иллюстрирует транспортные свойства этой схемы.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
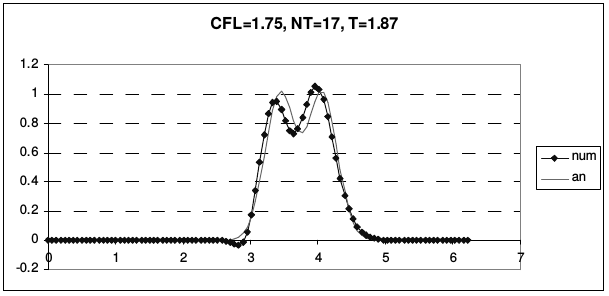 |
| Рис. 23 | |