Все построенные на равномерной сетке разностные операторы являются однородными - их коэффициенты в вычислительных шаблонах инвариантны относительно сдвигов шаблона по сетке. Для однородных дискретных операторов можно построить частные решения в виде бегущих волн:
здесь \({\rm\; \; \; }q=\exp \left\{i\left({\rm\omega \tau }\right)\right\}\) - множитель переходана следующий временной слой.
Подставим (2.38) в разностный оператор схемы «уголок» (2.26). Получаем:
Соотношение, выражающее множитель перехода через параметры дискретного оператора, будем называть характеристическим уравнениемразностной схемы.
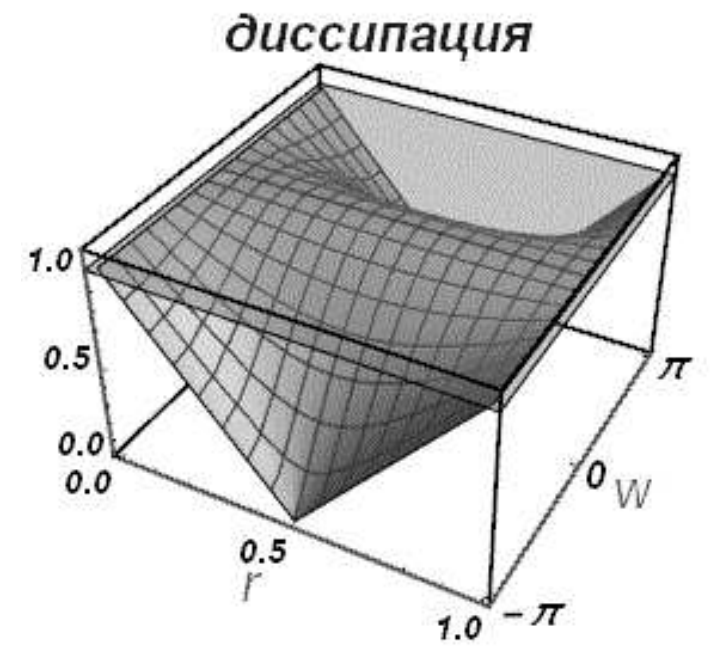
Модуль множителя перехода \(\left|q\right|\) является функцией от числа Куранта - Фридрихса-Леви \(r\) и приведенного волнового числа \(kh\), изменяющегося в пределах от \(-{\rm\pi }\): \(\left(-{\rm\pi }\le kh\le {\rm\pi }\right)\). Он показывает, как изменяется амплитуда бегущей волны при переходе на следующий слой. Если модуль перехода меньше или равен единице, то амплитуда волны не возрастает. Если для заданного \(r\) амплитуды всех волн при \(\left(-{\rm\pi }\le kh\le {\rm\pi }\right)\) не возрастают, то говорят, что данное число \(r\) принадлежит области устойчивости дискретного оператора. Опираясь на (2.39) можно показать, что область устойчивости разностной схемы «уголок» представляет собой единичный отрезок \(r\in \left[0,1\right]\). Если в области устойчивости модуль перехода любой волны равен единице, то дискретный оператор называется бездиссипативным, в противном случае имеет место численная диссипация.
Диссипативные свойства дискретного оператора для всех приведенных волновых чисел наиболее наглядно можно представить в виде двумерной поверхности \(\left|q\right|=f\left(r,kh\right)\). Для схемы «уголок» диссипативная поверхность изображена на рис. 6а, где по оси \(z\) отложены значения модуля перехода, по оси \(x\) - значения числа \(r\in \left[0,1\right]\), по оси \(y\) - значения приведенного волнового числа \(kh\in \left[-{\rm\pi },{\rm\pi }\right]\). Видно, что модуль перехода стремится к единице для длинноволновых гармоник, для которых \(kh\approx 0\), и равен единице на границе области устойчивости, при \(r=1,{\rm\; }\left(-{\rm\pi }\le kh\le {\rm\pi }\right)\).
 |
 |
| а) | б) |
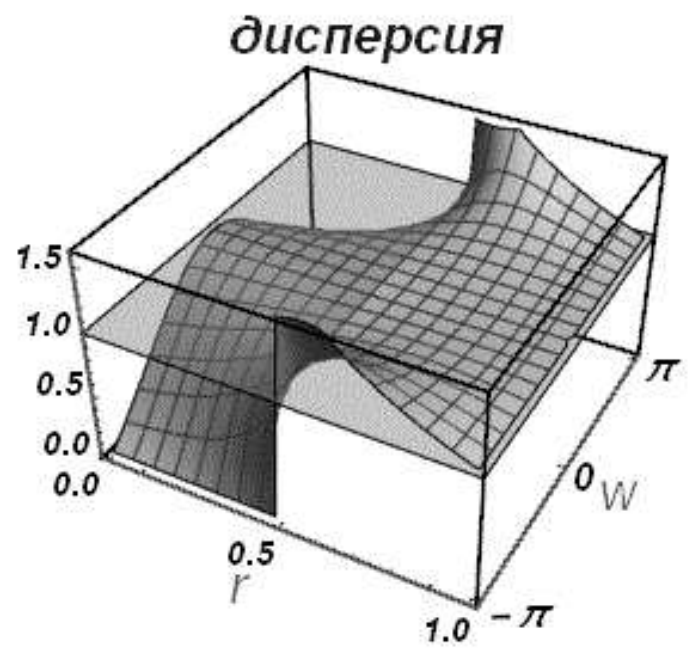
| Рис. 6. Диссипативная и дисперсионная поверхности схемы «уголок» | |
Из (2.39) также следует дисперсионное соотношение:
откуда получается выражение для приведенной фазовой скорости бегущих волн:
Приведенная фазовая скорость бегущих волн, описываемых исходным дифференциальным оператором, не зависит от номера гармоники и равна единице. Как ранее уже отмечалось, зависимость фазовой скорости от длины волны называется дисперсией. В разностном случае приведенная фазовая скорость может принимать значения как меньшие, так и большие единицы. В первом случае дисперсия называется «нормальной», во втором - «аномальной». В случае нормальной дисперсии гармоника отстает от «эталонной» гармоники, двигающейся с фазовой скоростью \(c\), в случае аномальной дисперсии - опережает ее.
Дисперсионные свойства дискретного оператора представляются его «дисперсионной поверхностью». На рис. 6в приведена дисперсионная поверхность разностного оператора «уголок». Здесь по оси \(z\) отложены значения приведенной фазовой скорости \({\rm\gamma }\), по оси \(x\)- значения числа \(r\in \left[0,1\right]\), по оси \(y\) - значения приведенного волнового числа \(kh\in \left[-{\rm\pi },{\rm\pi }\right]\). Дисперсия стремится к нулю, что соответствует стремлению \({\rm\gamma }\) к единице, для длинноволновых гармоник, для которых \(kh\approx 0\) и на границе области устойчивости, при \(r=1,{\rm\; }\left(-{\rm\pi }\le kh\le {\rm\pi }\right)\).
Стремление к нулю дисперсии и диссипации длинноволновых гармоник является общим свойством всех дискретных операторов, аппроксимирующих исходный дифференциальный оператор. Характер касания дисперсионных и диссипативных поверхностей единичной плоскости определяется порядком аппроксимации разностного оператора. Тот факт, что при \(r = 1\)все гармоники не диссипируют и не диспергируют, говорит о том, что разностный оператор при данном числе Куранта переносит начальный профиль без каких либо искажений.
Из непрерывности дисперсионной и диссипативной поверхностей следует, что в некоторой окрестности этого числа точность численного решения также будет аномально высокой и эту область можно назвать «каналом высокой точности» дискретного оператора.
Из рис. 6в видно, что дисперсия схемы «уголок» при \(r < 0.5\) является нормальной, а при \(r > 0.5\) - аномальной. При \(r = 0.5\)дисперсия отсутствует.
Диссипативная и дисперсионная поверхности дают полное представление о свойствах разностной схемы, позволяют предсказывать поведение дискретного решения на разных начальных условиях. Рассмотрим модельную задачу (2.1) с периодическими начальными условиями на отрезке \(x\in \left[0,2{\rm\pi }\right]\):
и двумя видами начальных условий - достаточно гладкими и разрывными.
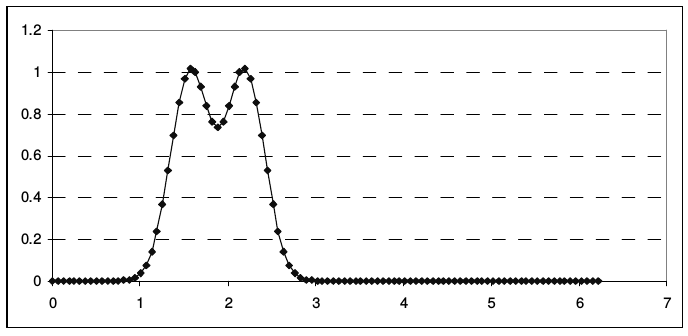
В качестве гладкого начального условия возьмем «двойной гауссиан» с параметрами:
в качестве разрывного - «ступеньку»:
Аппроксимируем дифференциальную задачу (2.40) - (2.42) разностной схемой «уголок». Разобьём отрезок \(x\in \left[0,2{\rm\pi }\right]\) на N=100 равных интервалов с шагом \(h=0.2{\rm\pi }\) и спроектируем на нее начальные данные (2.41) - (2.42):
Разложим эти сеточные функции в ряд Фурье:
где коэффициенты разложения определяются по формуле:
На рис. 7 представлены графики начальных данных (2.43), на рис. 8 - модули их коэффициентов разложения \(a_{k}^{\left(m\right)}\).
 |
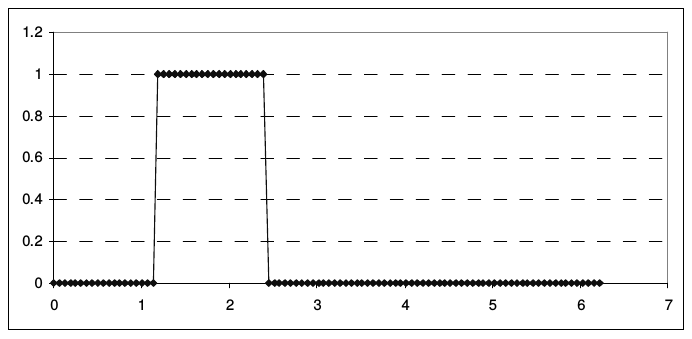 |
| Рис. 7 | |
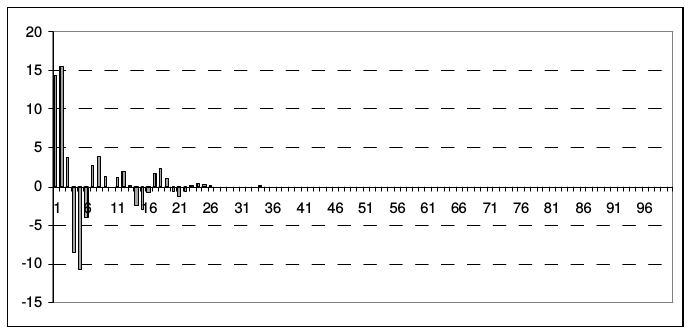 |
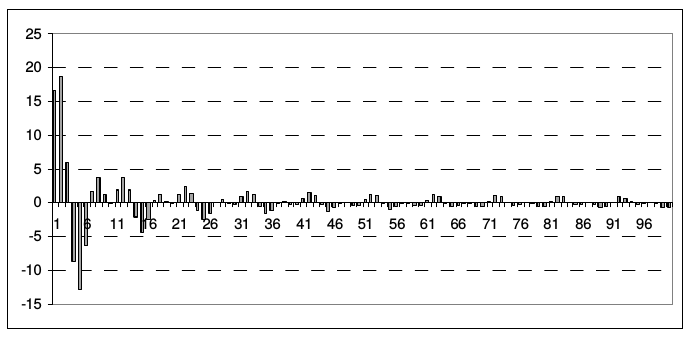 |
| Рис. 8 | |
В начальный момент времени все гармоники разложения (2.44) подогнаны друг к другу так, что в сумме составляют начальные данные. В последующие моменты времени каждая гармоника будет уменьшаться в амплитуде в соответствии с ее местом на диссипативной поверхности, и распространяться со своей фазовой скоростью, определяемой дисперсионной поверхностью, так что «пакет» гармоник начнет разъезжаться. Полная картина будет еще зависеть от числа Куранта-Фридрихса-Леви \(r\).
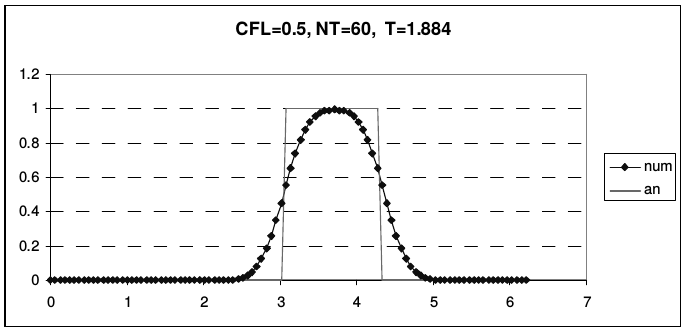
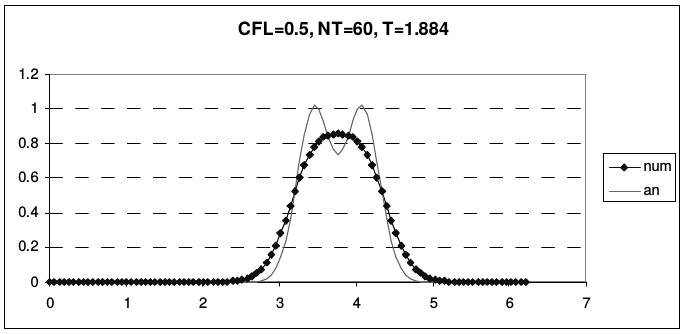
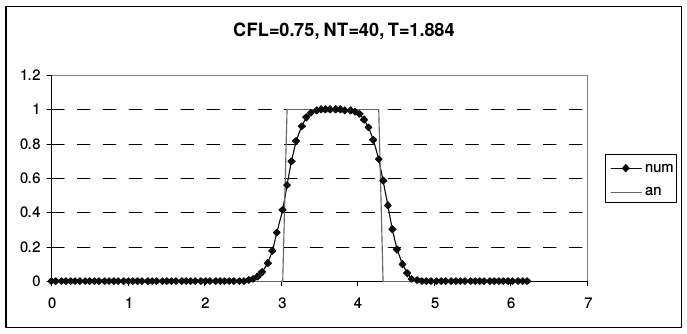
Из рис. 6 видно, что наибольшая диссипация высоких гармоник имеет место при \(r = 0.5\). На рис. 9 приведен результаты расчета переноса начальных профилей (2.43), рассчитанные по схеме «уголок» при разных числах Куранта, до одного и того же момента времени. Сплошной линией показано аналитическое решение дифференциальной задачи, линией с маркерами - решение, рассчитанное по разностной схеме.
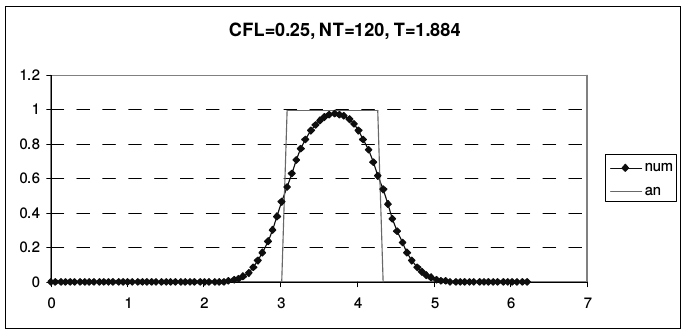 |
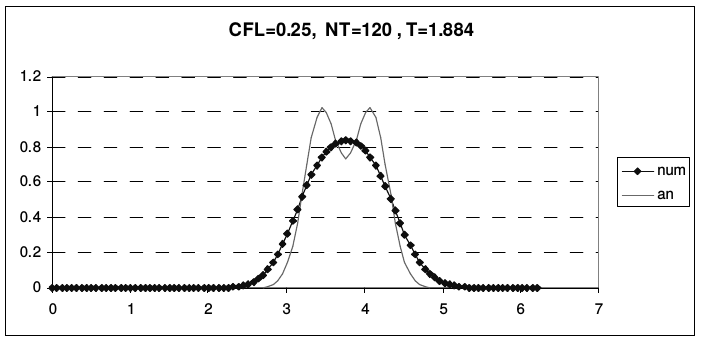 |
 |
 |
 |
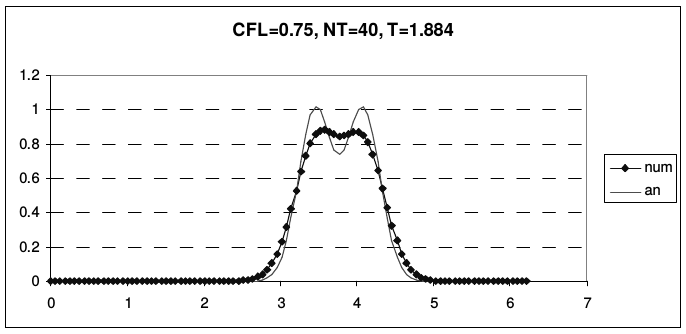 |
| Рис. 9. Результаты расчета по схеме «уголок» (Simplest Upwind) | |