← Назад Далее →

2.8. Схема «крест»

Характеристическое уравнение схемы «крест», в отличие от случаев, рассмотренных ранее, является квадратным трехчленом

$$q^{2} -2i\cdot qr\cdot \sin \left(kh\right)-1=0 (2.48)$$

и имеет два различных корня:

$$q_{1,2} =-ir\sin \left(kh\right)\pm \cdot \sqrt{1-r^{2} \sin ^{2} \left(kh\right)} (2.49)$$

Такая ситуация является типичной для всех трехслойных схем и отражает тот факт, что для трехслойной схемы начальные условия необходимо задавать на двух первых слоях.

Полное решение разностной задачи по трехслойной схеме можно представить в виде суммы двух рядов Фурье:

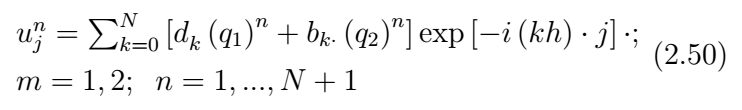
На нулевом слое по времени это разложение должно совпадать с начальным условием:

$$f_{j}^{} =\sum _{k=0}^{N}\left[d_{k}^{} +b_{k\cdot } \right]\exp \left[-i\left(kh\right)\cdot j\right] ,\quad \Rightarrow \quad d_{k}^{} +b_{k\cdot } =a_{k}$$

Будем называть один из корней характеристического уравнения «реальным», а второй - «паразитным». Закрепим за реальным корнем обозначение \(q_1\), за паразитным - \(q_2\). При идеально согласованном задании данных на нулевом и первом слоях по времени амплитуды каждой из гармоник должны умножиться на q₁. При отсутствии идеального согласования появится рассогласование, величину которого обозначим как \({\rm\delta }_{k}\):

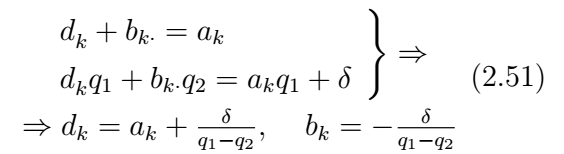
откуда следует, что паразитный корень описывает эволюцию во времени начального рассогласования начальных данных. Если модуль паразитного корня меньше единицы, то ошибка согласования со временем затухает.

Для каждого из корней характеристического уравнения можно построить свою диссипативную и дисперсионную поверхности. Возникает вопрос, какой именно из двух корней является «реальным», а какой «паразитным»?

Реальный корень определяет решение, аппроксимирующее исходный дифференциальный оператор, поэтому его диссипативная и дисперсионные поверхности должны «прижиматься» к единице при стремлении приведенного волнового числа к нулю при всех числах Куранта из области устойчивости.

Паразитный корень, напротив, реального решения не описывает и указанного асимптотического поведения не проявляет. Однако, для устойчивости расчетов, его модуль не должен превышать единицу.

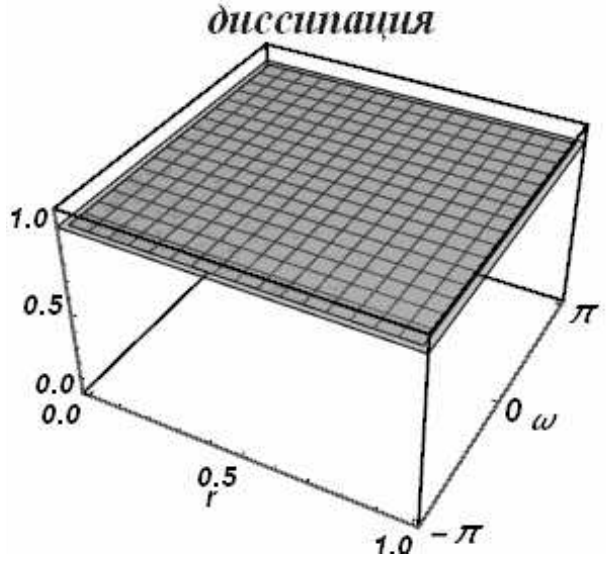
Из формулы (2.49) легко получить, что при \(\left|r\right|\le 1\)модули обоих корней равны единице, что говорит о бездиссипативности схемы при всех волновых числах. На рис. 15 приведены диссипативная и дисперсионная поверхности «реального» корня, на рис. 16 - «паразитного»

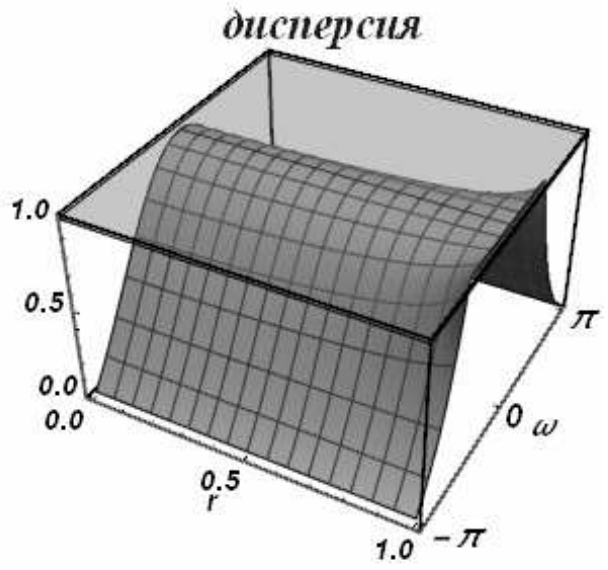Рис. 15

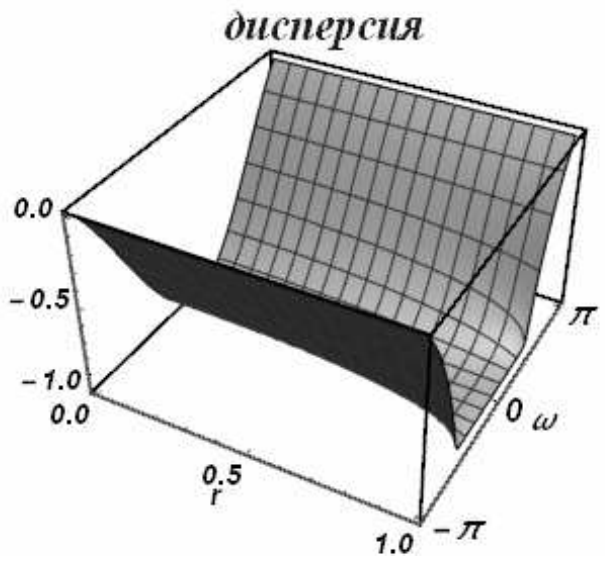Рис. 16

Из рис. 15 видно, что схема «крест» при всех числах Куранта имеет нормальную дисперсию.

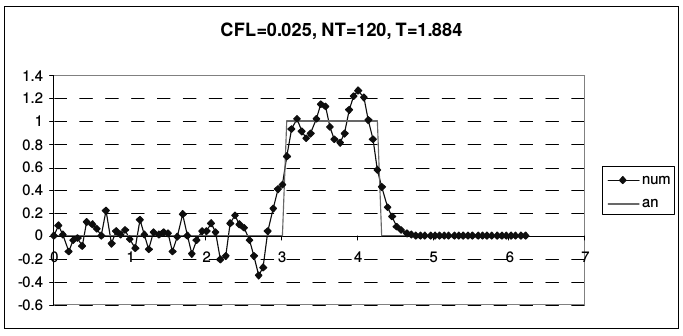
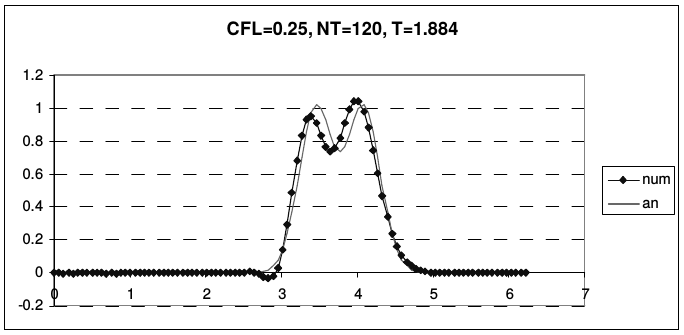
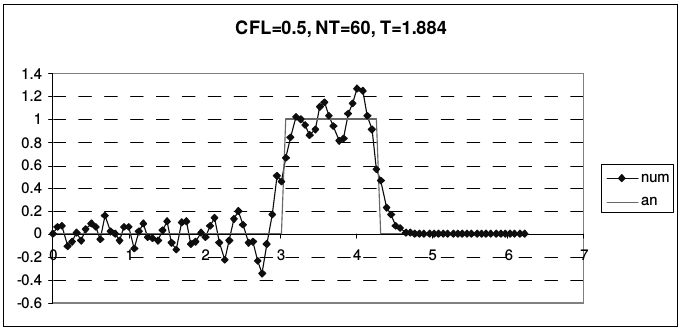
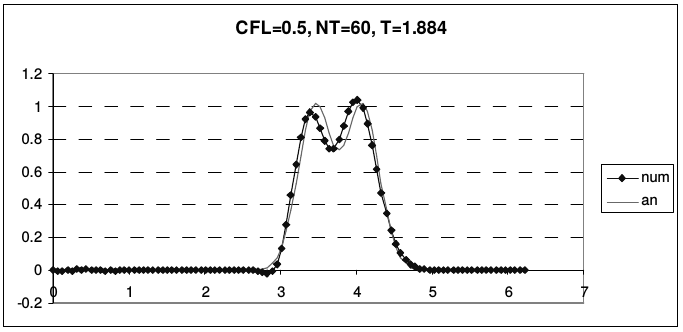
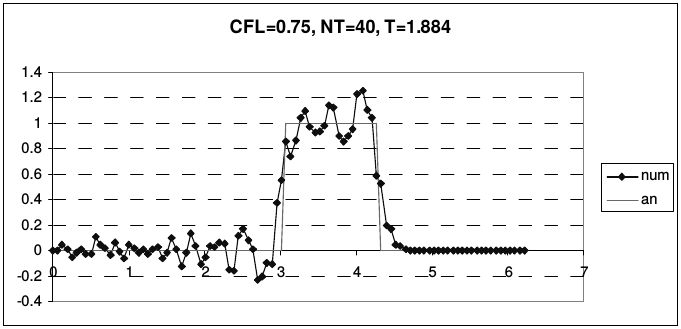
На рис. 17 приведены результаты использования схемы «крест» для решения уравнения переноса стандартных профилей при разных числах Куранта.

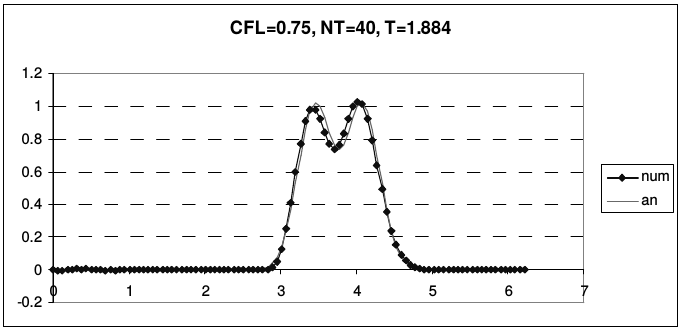Рис. 17. Результаты расчетов по схеме «крест» (Leap-Frog)

← Назад Далее →