← Назад Далее →

2.11. Схема Абрашина-Самарского

Эта схема является модификацией схемы «неявный уголок» (рис. 2,В), безусловно устойчивой схемы первого порядка аппроксимации с большой схемной вязкостью и имеет вид:

$$\frac{u_{i}^{n+1} -u_{i}^{n} }{{\rm\tau }} +\frac{c}{2} \cdot \left(\frac{u_{i}^{n+1} -u_{i-1}^{n+1} }{h} +\frac{u_{i+1}^{n} -u_{i}^{n} }{h} \right)=0 (2.54)$$

Добавление дополнительной точки с текущего слоя в вычислительный шаблон наделяет ее вторым порядком аппроксимации и уничтожает схемную вязкость. Характеристическое уравнение для схемы Абрашина-Самарского можно записать как:

$$q=\frac{\left[2+r\left({\rm e}^{{\rm i}w} -1\right)\right]}{\left[r-\left(r-2\right){\rm e}^{{\rm i}w} \right]} \cdot {\rm e}^{{\rm ikh}} (2.55)$$

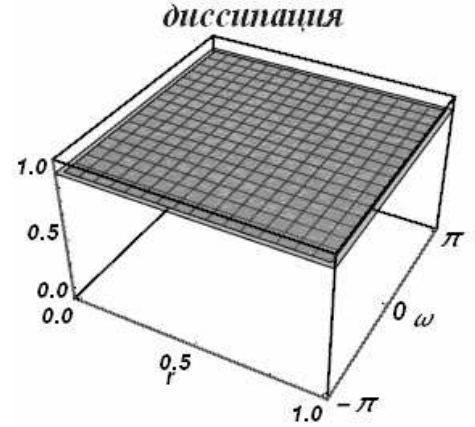
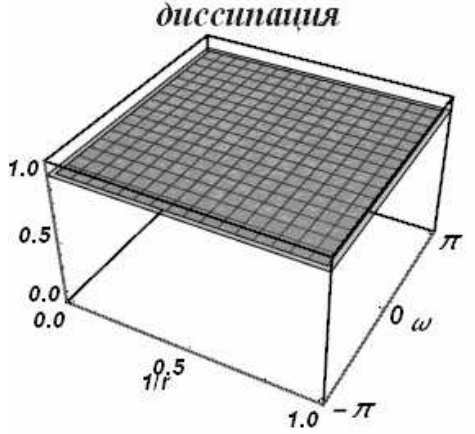
Схема безусловно устойчива, т.е. устойчива на полуоси \(0\le r<\infty\). Ее диссипативные и дисперсионные поверхности приведены на рис. 24, 25.

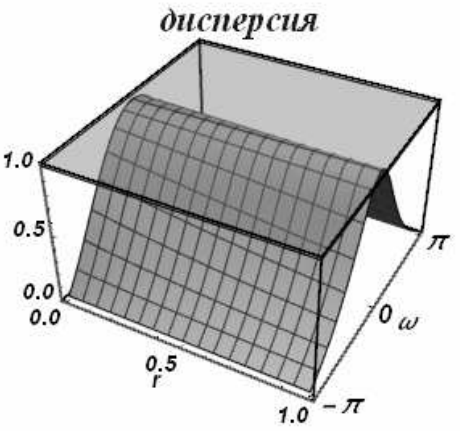а)	б)
Рис. 24

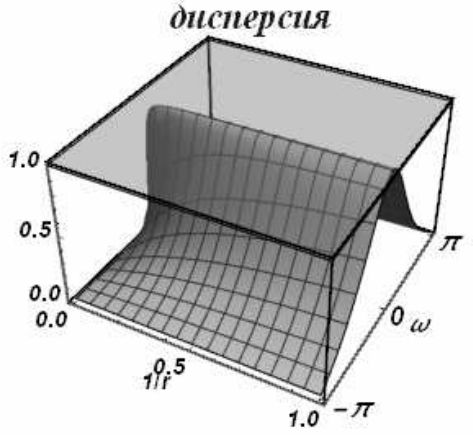а)	б)
Рис. 25

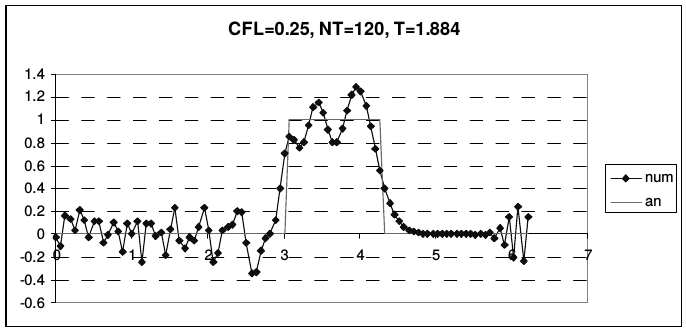
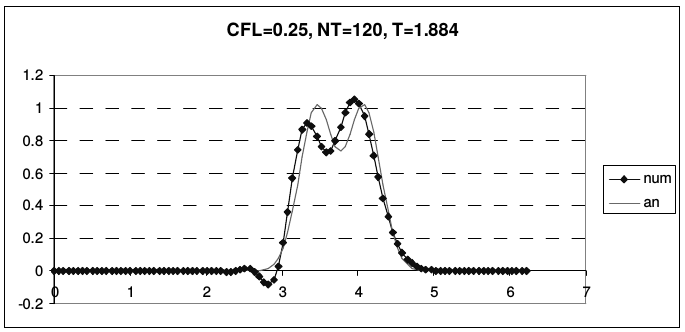
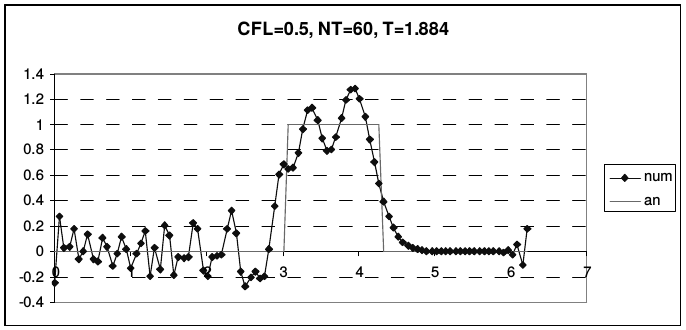
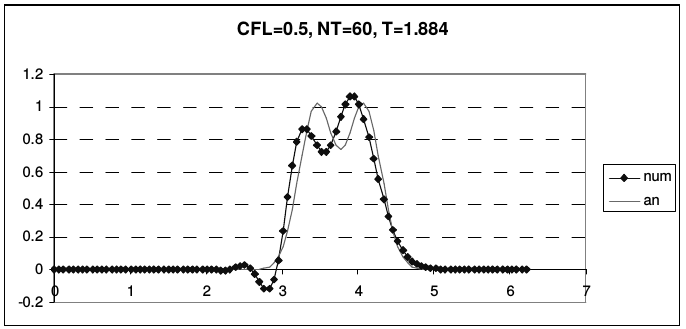
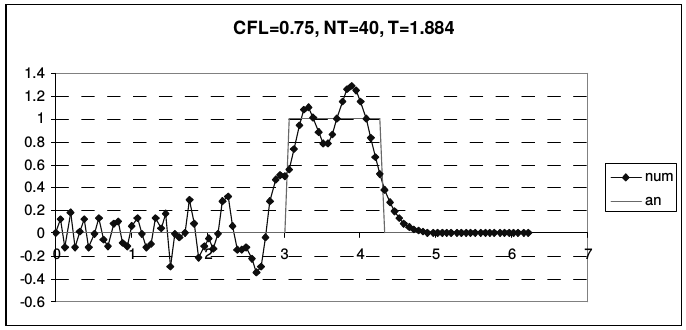
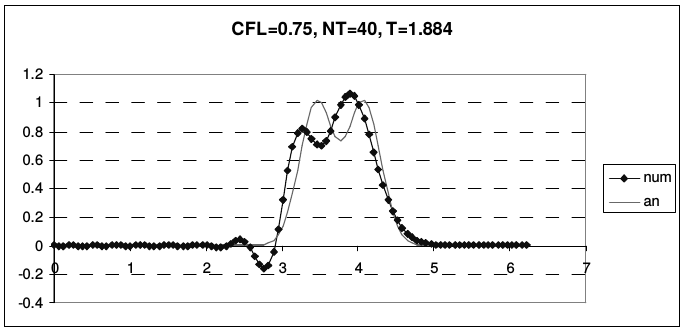
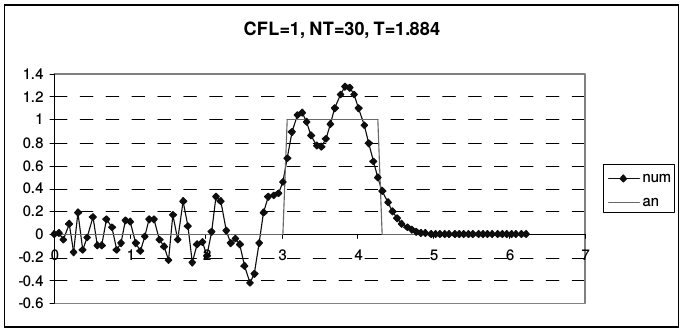
В отличие от предыдущих случаев, эта схема не является точной при числе Куранта \(r = 1\). Во всей области устойчивости схема обладает сильной нормальной дисперсией. На рис. 26 представлены результаты расчета тестовой задачи по схеме Абрашина-Самарского.

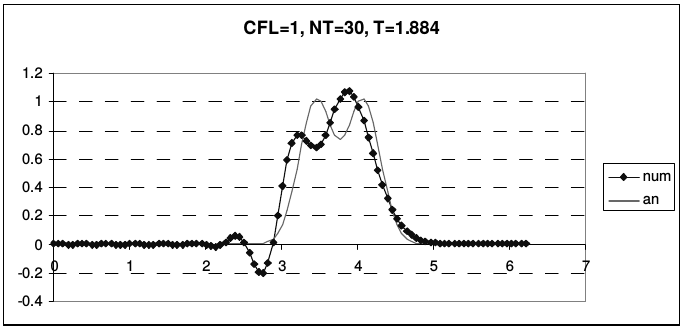Рис. 26

 

← Назад Далее →