На множестве дифференцируемых функций \(C^1\), определенных на пространственно-временной плоскости \(\left(x,t\right)\), простейшее линейное уравнение в частных производных можно записать как:
где \(c = const\) - произвольное действительное число \(c \in R\). Действительно, простейшее уравнение должно содержать частные производные по обеим переменным, иначе оно будет обыкновенным дифференциальным уравнением. Требование линейности приводит к тому, что частные производные должны объединяться в уравнении посредством операций сложения или вычитания. Введение действительного числа \(c = const\), которое может принимать как положительные, так и отрицательные значения, объединяет обе эти операции.
Общее решение уравнения (1.1) имеет вид:
что легко проверить непосредственной подстановкой. Конкретный вид функции \(f\)определяется начальными и граничными условиями.
Частный случай общего решения, когда
называется бегущей волной. Величины \(\omega\) и \(k\) называются круговой частой и волновым числом соответственно. Величину \({{\rm\omega }\mathord{\left/ {\vphantom {{\rm\omega } k}} \right. } k}\) называют фазовой скоростью бегущей волны. Подстановка (1.3) в (1.1) приводит к дисперсионному соотношению \({{\rm\omega }\mathord{\left/ {\vphantom {{\rm\omega } k}} \right. } k} =c\), означающему, что все бегущие волны, удовлетворяющие уравнению переноса (1.1), имеют одинаковую фазовую скорость. Величину c называют скоростью переноса.
Уравнение (1.1) можно представить также в другом виде:
где
Из представления (1.4) следует, что \({\rm\phi }=const\) вдоль каждой прямой на плоскости \(\left(x,t\right)\), определяемой уравнением:
Прямые (1.6) называются характеристиками уравнения (1.1), а само уравнение (1.1) называют уравнением переноса.
Следует отметить, что представление уравнения переноса в виде обыкновенных дифференциальных уравнений вдоль характеристик (1.4) дает возможность отказаться от требования дифференцируемости решения по переменным \(x\) и \(t\).
Постановка задач на основе уравнения переноса (1.1) включает в себя задание области \(G\), в которой ищется решение, и начальных и граничных условий.
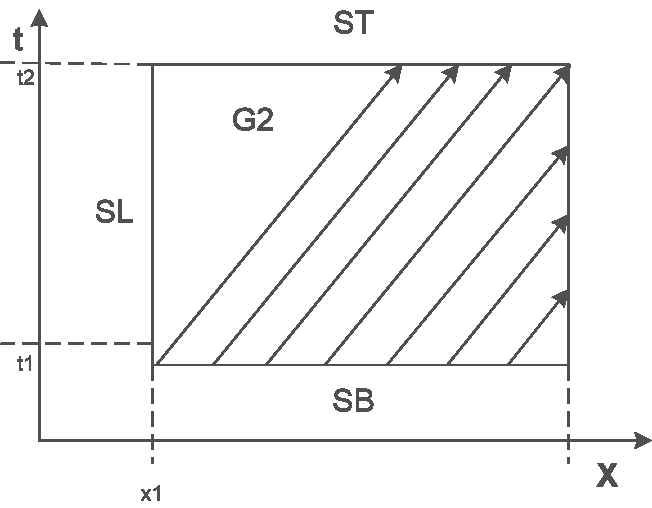
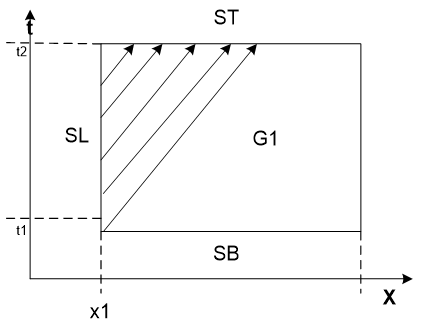
Пусть область \(G\) представляет собой прямоугольник \(G:\left[x_{1} ,x_{2} \right]\times \left[t_{1} ,t_{2} \right]\). Обозначим \(S_{L} ,S_{R} ,S_{T} ,S_{B}\) левую, правую, верхнюю и нижнюю границы этого прямоугольника соответственно (рис.1). В этом случае характеристики, пересекающие нижнюю границу прямоугольника \(G\), сплошь покроют подобласть \(G_1\) (рис. 1). Вдоль каждой из этих характеристик функция \({\rm\phi }\) будет постоянной и равной значению \({\rm\phi }\left(x,t_{1} \right)\) в точке ее пересечения с отрезком \(x\in \left[x_{1} ,x_{2} \right]\). Подобласть \(G_2\) покроют характеристики, пересекающие левую границу области \(G\). Функция \({\rm\phi }\) вдоль этих характеристик также будет постоянной, равной ее значениям в точках пересечения с границей \(S_{L}\). Таким образом, для однозначного определения решения уравнения переноса в области \(G\), необходимо задать значения функции \({\rm\phi }\) на нижней и левой границах \(S_{B}\) и \(S_{L}\):
 |
 |
| а) | б) |
| Рис. 1 | |
Первое из этих условий можно считать начальным, второе - граничным. Возможность представления уравнения (1.1) в виде (1.4) позволяет не вводить ограничений на гладкость начальных и граничных условий - функции \({\rm\theta }\left(x\right)\) и \({\rm\psi }\left(t\right)\)могут не иметь производных ни в одной точке их определения.
Значения решения на границах \(S_{R}\) и \(S_{T}\) однозначно определяются по начальным и граничным условиям (1.7).