← Назад Далее →

2.3. Метод неопределенных коэффициентов

Множество разностных схем, аппроксимирующих уравнение (2.1), не исчерпывается приведенными в (2.3). Если отвлечься от «конечных разностей», то все схемы, рассмотренные выше, можно представить в виде:

$$\sum _{m\in stensil}{\alpha }_m\cdot u{}_m=0(2.19)$$

где суммирование проводится по заданному вычислительному шаблону (см. примеры рис. 2). Так для разностной схемы A («уголок»)

$${\alpha }_i^{n+1}=\frac{1}{\tau },{\alpha }_i^n=\frac{c}{h}-\frac{1}{\tau },{\alpha }_{i-1}^n=-\frac{c}{h},(2.20)$$

для схемы G («крест»)

$${\alpha }_i^{n+1}=\frac{1}{2\tau },{\alpha }_{i+1}^n=\frac{c}{2h},{\alpha }_{i-1}^n=-\frac{c}{2h},{\alpha }_i^{n-1}=-\frac{1}{2\tau }(2.21)$$

Для нахождения коэффициентов ${\alpha }_m$ по заданному шаблону можно использовать т.н. «метод неопределенных коэффициентов», суть которого заключается в том, что дифференциальный и разностный (дискретный) операторы должны одинаковым образом действовать на некоторое множество полиномов от переменных $x,t$:

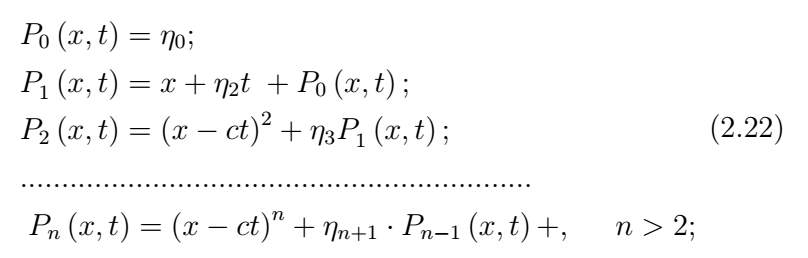
где ${\eta }_j,j=1,2,...,n$произвольные константы. Максимальный порядок полинома, на который дискретный и дифференциальный операторы действуют одинаковым образом, будем называть порядком аппроксимации дискретного оператора.

Из этого определения следует, что для того, чтобы дискретный оператор обладал первым порядком аппроксимации, его коэффициенты должны удовлетворять условиям:

$$\sum _{m\in stensil}{\alpha }_m=0;\sum _{m\in stensil}{x}_m\cdot {\alpha }_m=c;\sum _{m\in stensil}{t}_m\cdot {\alpha }_m=1;(2.23)$$

Если вычислительный шаблон оператора состоит из трех узлов, то условия (2.23) позволяют однозначно определить неизвестные коэффициенты ${\alpha }_m$.

Так для шаблона А (рис. 1) получаем:

$$\begin{array}{l}{\alpha }_{i-1}^n+{\alpha }_i^n+{\alpha }_i^{n+1}=0;\\ (x_i-h){\alpha }_{i-1}^n+({\alpha }_i^n+{\alpha }_i^{n+1})x_i=c;\Rightarrow {\alpha }_{i-1}^n=-c/\phantom{ch}h;\\ t_n({\alpha }_{i-1}^n+{\alpha }_i^n)+{\alpha }_i^{n+1}(t_n+\tau )=1;\Rightarrow {\alpha }_i^{n+1}=1/\phantom{1\tau }\tau ;\\ \end{array}$$

откуда следует (2.20). Аналогичным образом можно получить коэффициенты дискретных операторов и для шаблонов B, C, D.

При увеличении числа узлов в шаблоне на единицу можно получать дискретные операторы второго порядка аппроксимации. Для этого, наряду с (2.23), нужно выполнить условие:

$$\sum _{m\in stensil}{(x-ct)}_m^2\cdot {\alpha }_m=0;(2.24)$$

Применим это правило к шаблону G схемы «крест». Система уравнений (2.23), (2.24) в этом случае примет вид:

$$\begin{array}{l}{\alpha }_{i-1}^n+{\alpha }_{i+1}^n+{\alpha }_i^{n+1}+{\alpha }_i^{n-1}=0;\\ (x_i-h){\alpha }_{i-1}^n+({\alpha }_i^{n+1}+{\alpha }_i^{n-1})x_i+(x_i+h){\alpha }_{i+1}^n=c;\Rightarrow {\alpha }_{i+1}^n-{\alpha }_{i-1}^n=-c/\phantom{ch}h;\\ t_n({\alpha }_{i-1}^n+{\alpha }_{i+1}^n)+{\alpha }_i^{n+1}(t_n+\tau )+{\alpha }_i^{n-1}(t_n-\tau )=1;\Rightarrow {\alpha }_i^{n+1}-{\alpha }_i^{n-1}=1/\phantom{1\tau }\tau ;\\ ({\alpha }_{i-1}^n+{\alpha }_{i+1}^n)h^2+({\alpha }_i^{n+1}+{\alpha }_i^{n-1})c^2{\tau }^2=0;\end{array}$$

Условие (2.24) здесь преобразовано с учетом трех предшествующих условий. Разрешая приведенную систему, получаем решение, совпадающее с (2.21). Аналогично могут быть вычислены коэффициенты для шаблона E (схема Карлсона). Однако, описанный метод, примененный к шаблону F, приводит к другой схеме, схеме Лакса - Вендроффа, обладающей вторым порядком аппроксимации как по времени, так и по пространству. Схема с «симметричной аппроксимацией конвективных потоков», имеющая порядок аппроксимации $O(\tau +h^2)$, может быть получена, если вместо (2.24) потребовать выполнения условия $\sum _{m\in stensil}{x}_m^2\cdot {\alpha }_m=2c{x}_i^n$.

Следует отметить, что при построении методом неопределенных коэффициентов схем со вторым порядком аппроксимации и выше использовалось частное решение исходного дифференциального уравнения $u=F(x-ct)$. По этой причине такие аппроксимации называются «аппроксимациями на решении». При построении схем первого порядка частное решение не используется.

Наряду с понятием аппроксимации на решении можно ввести понятие «строгой аппроксимации оператора», не опирающееся на его частные решения. Будем считать, что дискретный оператор строго аппроксимирует исходный дифференциальный оператор с порядком $n$, если области их значений совпадают на полном множестве полиномов степени $n$:

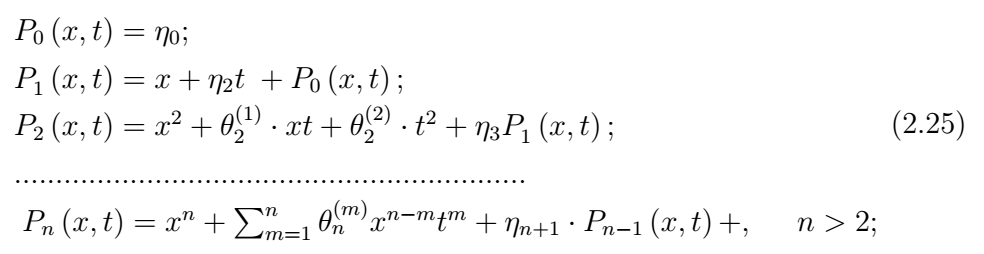
Множество полиномов (2.22) является в этом смысле не полным.

Схемы первого порядка всегда строго аппроксимируют исходные дифференциальные операторы. Для аппроксимации дифференциального оператора на решении с порядком $n>2$ достаточно $n+2$ узлов в вычислительном шаблоне, для строгой аппроксимации требуется $(n+2)(n+1)/2\$$узлов.

При построении разностных схем можно ориентироваться не только на максимально возможный порядок аппроксимации. Так схемы типа (2.19) можно строить следующим образом: для данного числа точек на $n$-ом временном слое ищется схема, обладающая порядком аппроксимации на решении, на единицу меньшим максимально возможного. В результате получается система уравнений, число неизвестных в которой на единицу больше числа уравнений. Оставшимся свободным параметром можно распорядиться таким образом, чтобы улучшить дисперсионные и диссипативные свойства разностной схемы.

Метод неопределенных коэффициентов естественным образом обобщается на неравномерные расчетные сетки. При выборе вычислительного шаблона следует обращать внимание на его компактность и корректное отображение области зависимости решения (свойство «транспортивности» схемы, П. Роуч) - при $c>0$решение уравнения переноса не должно зависеть от значений переменных, находящихся справа от точки, в которой ищется решение.

Построение дискретных операторов, аппроксимирующих дифференциальный оператор переноса с высоким порядком, методом неопределенных коэффициентов связано с большим объемом алгебраических выкладок и редко применяется на практике.

← Назад Далее →